Conceitos básicos sobre o som.

A contínua evolução dos sistemas de sonorização vem permitindo produzir cada vez melhor todos os níveis sonoros. Com a ampliação da faixa de níveis sonoros que se pode reproduzir, é necessário aprimorar a qualidade do material de áudio, o que pode ser feito usando-se uma grande variedade de equipamentos digitais e analógicos, que efetuam processamentos adequados ao áudio que se quer reproduzir.

1.1 – Níveis sonoros

Para entender como esses processadores atuam, é necessário compreender primeiro alguns conceitos sobre o áudio e como funciona a dinâmica do som.

Em qualquer processador de dinâmica (ex: Behringer Ultramizer), a quantidade de amplificação ou atenuação é expressa em decibéis (dB).

A abreviatura dB não é uma unidade de medida (embora freqüentemente seja usada como tal). Na verdade, ela descreve uma relação logarítmica entre dois valores. A faixa total dos níveis da audição do ser humano, desde o limiar da audição até o estrondo de uma turbina de avião (veja Fig.1), varia desde cerca de 0,00002 Pa até 130 Pa (já no limiar da dor).

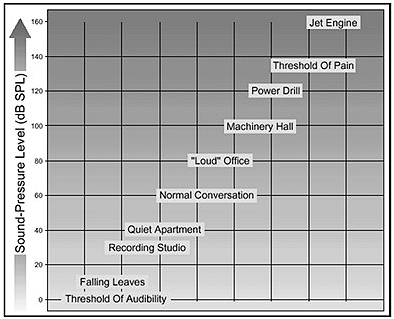
Figura 1: Faixa dinâmica da audição do ser humano

Pode-se observar, portanto, que a faixa total de níveis de pressão sonora (medidos em Pa) percebidos pelo ouvido humano engloba uma variação da ordem de 10.000.000 vezes. Por ser muito difícil trabalhar com uma faixa tão grande de valores e como a percepção humana dos níveis sonoros não se dá numa variação linear, mas sim logarítmica, buscou-se então uma forma mais prática de representar as variações de pressão sonora.

O decibel é uma unidade que descreve uma relação enter dois níveis sonoros. Para ficar mais claro qual o tipo de quantidade que está sendo avaliada, é comum usar a sigla SPL (“sound pressure level” – nível de pressão sonora) junto com a sigla dB. Assim, partindo-se do valor de 0 dBSPL (2-10 Pa) como sendo o limiar da audição, qualquer valor de dB pode ser calculado pela seguinte fórmula:

L = 20.log (P2 / P1)

onde:
L = valor absoluto do nível sonoro em dBSPL
P1 = nível de pressão sonora de referência (0,00002 Pa)
P2 = nível de pressão sonora (em Pa) produzido pela fonte sonora que se deseja medir
log = logaritmo decimal

É importante saber que 0 dB não significa silêncio absoluto, que seria referido como “menos infinito”.

Como pode ser observado, o ouvido humano possui uma faixa dinâmica bastante ampla, variando cerca de 130 dB, e que ultrapassa a faixa disponível nos gravadores DAT e nos CDs, que é de cerca de 96 dB.

Do ponto de vista físico, um aumento de 3 dB corresponde a um aumento de potência de um fator de 2, enquanto que o ouvido humano só perceberá que o som está duas vezes mais forte quando este tiver sido aumentado em 10 dB.

É possível fabricar equipamentos de áudio analógicos com faixa dinâmica da ordem de 130 dB, mas a faixa dinâmica dos equipamentos digitais de 16 bits é cerca de 25 dB menor. Os gravadores convencionais de fita e os sistemas atuais de televisão e radiodifusão possuem faixa dinâmica ainda menor. Em geral, as restrições de faixa dinâmica são conseqüência dos ruídos inerentes à mídia de armazenamento ou ao processo de transmissão, e também por causa do headroom desses sistemas.

Figura 2: Capacidade dinâmica de vários dispositivos

1.2 – O ruído como fenômeno físico

Todo componente elétrico produz um certo nível de ruído. O fluxo da corrente elétrica através de um condutor cria movimentos aleatórios de elétrons, que geram freqüências dentro de todo o espectro de áudio. Se essas correntes forem muito amplificadas, o resultado será percebido como ruído. Uma vez que todas as freqüências são igualmente afetadas, esse ruído é chamado de ruído branco (“white noise”). Como a eletrônica não pode funcionar sem seus componentes, mesmo quando se usam circuitos especiais de baixo ruído, sempre haverá um certo grau de ruído.

Esse efeito é similar na reprodução de uma fita de áudio, quando as partículas magnéticas não alinhadas que passam na cabeça de reprodução podem também causar tensões e correntes aleatórias. O som resultante das várias freqüências é percebido como ruído. Mesmo os gravadores com os melhores esquemas de polarização não podem conseguir uma relação sinal/ruído melhor do que 70 dB, o que é inaceitável nos padrões de hoje, em que os ouvintes estão mais exigentes. Por causa de suas limitações técnicas, os gravadores de fita magnética não podem ser mais melhorados usando-se os processos convencionais.

1.3 – A dinâmica do som

Como já foi apresentado, o ouvido humano pode perceber variações de amplitude muito grandes – desde o mais leve susurrar até o estrondo de um avião. Caso alguém tente gravar ou reproduzir todo esse amplo espectro de dinâmica por meio de amplificadores, gravadores cassete, discos ou mesmo gravadores digitais (CD, DAT, etc.), imediatamente encontrará as restrições devidas às limitações físicas da tecnologia eletrônica de reprodução de som.

A faixa dinâmica dos equipamentos eletroacústicso é limitada tanto no extremo inferior quanto no superior. O ruído térmico gerado pelo movimento dos elétrons nos componentes cria um piso de ruído (“noise floor”), que determina o limite inferior da faixa de transmissão. O limite superior, por sua vez, é determinado pelos níveis da tensão operacional interna do equipamento; se ela for ultrapassada, será ouvida uma distorção no sinal.

Embora na teoria a faixa dinâmica útil esteja entre esses dois limites, na prática ela é ainda menor, pois deve-se manter uma certa margem de reserva para evitar a distorção do sinal de áudio, caso ocorram picos momentâneos. Na linguagem técnica, essa margem de reserva é chamada de headroom, e em geral é de cerca de 10 a 20 dB.

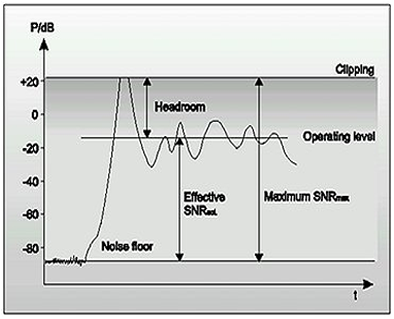Figura 3: Relação entre o nível operacional e o headroom

Para se ter um maior headroom, e assim reduzir o risco de haver distorção decorrente de picos no sinal, é necessário reduzir o nível operacional do sinal, o que, por outro lado, faz com que o piso de ruído seja aumentado consideravelmente. Por isso, é preciso manter o nível operacional o mais alto possível sem o risco de distorção do sinal, para que se obtenha uma transmissão com ótima qualidade.

1.4 – Digitalização do áudio

Para converter um sinal de áudio analógico (ex: sinal de um microfone) em códigos digitais, é usado um conversor analógico-digital (ADC). O conversor amostra várias vezes o sinal durante um período de tempo, digamos, 44.100 vezes por segundo, o que dá uma taxa de amostragem de 44.1 kHz. A cada amostragem, o conversor mede a amplitude do sinal e codifica-o sob a forma de valor numérico. Essa forma de medir o sinal regularmente durante um período de tempo é chamada de amostragem (“sampling”), e a conversão da amplitude do sinal em valor numérico é chamada de quantização (“quantize”). As duas ações juntas compõem o processo de digitalização.

Para fazer oposto – conversão do código digital em sinal analógico – é usado um conversor digital-analógico (DAC).

Em ambos os casos, a freqüência na qual o dispositivo opera é chamada de taxa de amostragem (“sampling rate”). A taxa de amostragem determina a resposta efetiva de freqüências, e deve ser mais do que o dobro da maior freqüência a ser reproduzida. Dessa forma, a taxa de amostragem de 44.1 kHz do CD é ligeiramente mais alta do que o dobro da freqüência mais alta de áudio, que é 20 kHz.

A precisão da quantização é diretamente dependente da qualidade dos conversores ADC e DAC. A resolução ou tamanho do número digital (expresso em bits) determina a relação sinal/ruído teórica que o sistema de áudio é capaz de operar. O número de bits pode ser comparado ao número de casas decimais de uma calculadora – quanto maior, mais preciso será o resultado.

Teoricamente, cada bit extra de resolução aumenta a relação sinal/ruído em cerca de 6 dB. Infelizmente, há ainda um número considerável de fatores que devem ser levados em conta, e que interferem no resultado final da qualidade.

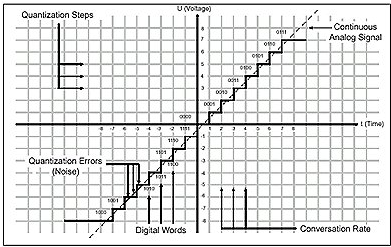Figura 4: Diagrama de transferência de um conversor analógico-digital linear ideal.

Se você representar um sinal analógico como uma função senoidal, então o procedimento de amostragem pode ser imaginado como uma grade aplicada à função. Quanto maior a taxa de amostragem e maior a quantidade de bits, mais fina será a grade. O sinal analógico traça uma curva contínua, que raramente coincide com os pontos de cruzamento das linhas da grade. É aferido um valor para cada ponto amostrado do sinal, que é então codificado digitalmente, o mais aproximado possível do ponto exato. O limite de resolução da grade (a distância entre os pontos de cruzamento das linhas) dá origem a erros, que causam o chamado ruído de quantização. Infelizmente, o ruído de quantização tem a característica de ser muito mais perceptível e desagradável ao ouvido do que os ruídos naturais do áudio analógico.

A digitalização do som possui um efeito colateral indesejável que é a alta sensibilidade à sobrecarga de sinal. Vejamos o seguinte exemplo: se um sinal analógico começa a sobrecarregar (saturar), ocorre que a amplitude do sinal atinge o nível máximo e os picos da onda começam a ser cortados (“clipping”). Quanto maior a proporção do sinal que está sendo cortado, mais harmônicos – percebidos como distorção – serão ouvidos. Esse processo é gradual, com o nível de distorção sendo uma percentagem do sinal total, e crescendo proporcionalmente ao aumento do sinal de entrada.

A distorção digital é diferente, como ilustra o exemplo bastante simples a seguir. Imagine uma situação onde um código de 4 bits possui o valor positivo 0111, e adicione a ele o menor valor possível (0001), que é o menor acréscimo de amplitude que pode haver. A adição dos dois códigos resulta no valor 1000, que indica o maior valor negativo possível. Ou seja, o valor que era positivo torna-se instantaneamente negativo (e máximo), resultando uma distorção extrema e bastante perceptível.

Nos processadores digitais de áudio, os dados serão modificados de diversas maneiras, com vários cálculos e processos, para se obter o efeito desejado. Isso dá origem a vários erros, uma vez que nesses cálculos os valores sofrem inevitáveis apoximações, resultando em mais ruído. Para minimizar esses erros de arredondamento, os cálculos devem ser efetuados com uma resolução maior do que a que os dados foram digitalizados, isto é, o processamento deve ser feito com uma resolução superior à dos conversores ADC e DAC. Por isso, muitos equipamentos processam com resolução interna de 24 bits, ou mesmo 32 bits, enquanto seus conversores possuem resolução de 16, 20 ou 24 bits.